L’introduzione delle frazioni nel percorso didattico dell’insegnamento della Matematica è giustificato dal fatto che i bambini/le bambine, nella vita quotidiana, incontrano situazioni che non si possono esprimere facendo riferimento ai soli numeri naturali. Il concetto di frazione è però molto complesso perché implica molti significati fra loro interconnessi. Alcuni di questi significati sono:
- è parte di un intero, che può essere continuo (per esempio la superficie di una figura) o discreto (cioè una quantità numerica come 7 penne, 7 caramelle…);
- è un operatore: 2/3 di 15 caramelle;
- esprime una percentuale: 25% = 25/100; anche se le due scritture formalmente sono fra loro equivalenti possiedono significati differenti tant’è che nella vita quotidiana la percentuale non si indica con la scrittura frazionaria;
- esprime una misura;
- in probabilità esprime il rapporto fra i casi possibili che accada un evento e quelli favorevoli;
- è un numero razionale;
- esprime un rapporto, una relazione fra due grandezze o quantità.
Nella Scuola Primaria si privilegia lo sviluppo dei primi 5 significati di frazione. Nel Sussidiario Mondo 2030 di cui siamo autrici sono state operate scelte che riteniamo importante esplicitare dal punto di vista teorico.
Nel significato di frazione come parte di un intero è essenziale una riflessione insieme agli alunni su cosa si intenda per “dividere un intero in parti uguali”. Mentre se dividiamo una quantità, l’aggettivo uguali significa “ugualmente numerosi” e questa suddivisione può essere effettuata in un solo modo, se dividiamo una superficie, significa di “uguale area”. Avere uguale area non vuol dire avere necessariamente anche uguale forma, essere cioè congruenti. Per evitare che i bambini/le bambine pensino alla frazione unicamente come a una divisione in parti congruenti, è importante avviare con loro una riflessione in tale senso e usare modelli nei quali la figura sia stata frazionata in parti equiestese, ma non congruenti. Le pagine di avvio al concetto di frazione presenti nel Sussidiario, sia nel volume di quarta che in quello di quinta, offrono spunto di riflessione in tale senso.
LEGGI ANCHE: L’entusiasmo degli insegnanti che usano Mondo 2030: “Sussidiario insostituibile, privo di rischi di misconcezioni”
Riteniamo inoltre che sia importante sviluppare il significato di frazione come parte di un tutto contemporaneamente, sia nell’ambito di grandezze continue che di quantità numeriche. Sebbene per i bambini/per le bambine sia più facile cogliere l’intero di riferimento se è una grandezza continua (una figura, un foglio, tavolette di cioccolata sono fra gli oggetti più usati e più vicini all’esperienza di tutti i bambini e le bambine), sviluppare inizialmente il concetto usando solo grandezze continue rischia di rendere più difficile trasferirlo al frazionamento di una quantità.
In quest’ottica sono state proposte le pagine 46, 47 e 48 del volume di classe quarta.

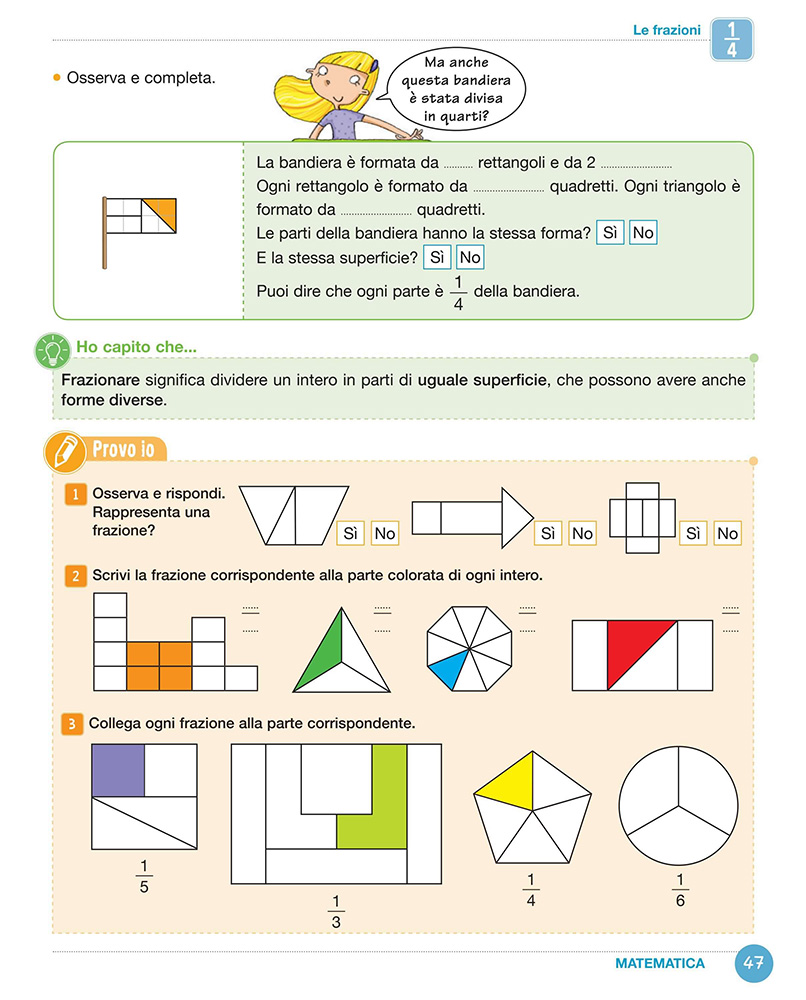

Per aiutare i bambini/le bambine a cogliere più facilmente l’intero anche nel caso in cui si frazionino quantità discrete, può essere di aiuto fare riferimento all’unità intera: “un pacchetto” con dentro 15 caramelle, “un sacchetto” con dentro 20 biscotti, “una scatola” con 12 cioccolatini.
Nello sviluppare il significato di frazione come rapporto fra uno/tutto, le definizioni di frazione propria, impropria, apparente non sono significative.
Riflettiamo su un esempio: 167/500 è una frazione propria. Se con il termine propria intendiamo che l’intero si può frazionare in 500 parti e ne possiamo considerare 167, ha senso dire che questa frazione è “propria” se fraziono una pizza o un foglio? Quando mai nell’esperienza quotidiana avviene una tale divisione?
La frazione 6/5 si dice che è “impropria” perché se dividi una tavoletta di cioccolata in 5 parti non ne puoi considerare 6. Ciò avviene però se l’intero è una tavoletta, ma se l’intero sono due tavolette allora diventa una frazione possibile.
LEGGI ANCHE: L’esito del sondaggio su facebook: Mondo 2030 è il sussidiario delle discipline da adottare
Evitiamo pertanto di indirizzare i bambini in meccanismi che sembrano semplificare (“guarda il numero che c’è al denominatore, se è … allora la frazione è …), ma che invece svuotano di significato un apprendimento e che, per questo, diventano oppositivi alla vera acquisizione di senso, mentre piuttosto concentriamoci sulla relazione e sul significato che di volta in volta vengono espressi dalla frazione. Secondo noi è opportuno stimolare i bambini a fare riferimento all’unità, parlando di frazioni minori, maggiori o uguali a 1, come proposto nel volume di quarta alle pagine 50, 51 e 52 e in quello di quinta a pagina 44. Inoltre è consigliabile introdurre e consolidare bene il concetto di frazione mediante esperienze concrete e quindi lavorare inizialmente con frazioni minori o uguali a 1 e solo successivamente introdurre le frazioni maggiori di 1. Tali frazioni non possiedono un significato immediatamente intuibile e per questo sono più difficili da capire: a volte l’intero è 1, ma a volte è formato da più interi, come nel caso della tavoletta di cioccolato di cui si parlava sopra.

MONDO 2030
Scopri il nuovo sussidiario del secondo ciclo della scuola primaria con la versione scientifica più adorata dagli insegnanti











